GRE数学の解き方に対するQ&A
[GRE数学完全攻略] 1.1.3 約数(Factors)
約数-応用問題5(MC2問題)


受講生の質問(1)
解説に書かれている”a^b=3^6が成立するには、bは6の約数となる。”と書いてありますが、なぜ6の約数となるのかが理解できません。
ジェイマス講師:J の回答(1)
a^bを素因数分解したものが3^6であり、a^b=3^6とするには、3^6を(整数)^(整数)という形に変形する必要があります。
- 3^6をそのまま捉えると、b=6 (a=3となる)、
- 3^6=3^(2×3)=(3^2)^3とすることで、b=3 (a=3^2となる)、
- 3^6=3^(3×2)=(3^3)^2とすることで、b=2 (a=3^3となる)、
- 3^6=(3^6)^1と捉えると、b=1 (a=3^6となる)
となります。
以上のようにbは3^6の指数である6を整数の掛け算に分解し、一部を3^(整数)としてaに分配、残りをaの指数であるbに分配するので、bは必ず6の約数となります。
倍数-基本問題1(MC1問題)

受講生の質問(1)
解説に、”p=20k=2^2×5kと表すことができるが、〜選択肢は整数になる。”と書いてありますが、その文章中の、”2の指数に着目するとkは2^3÷2^2=2の倍数をとりえない。”がどういう意味なのか理解できません。
ジェイマス講師:J の回答(1)
p=20k=2^2×5kについて、もしこれが8=(2^3)の倍数であるとすると、2の指数を3以上持つ必要があります。
p=2^2×5kのうち、2の指数が2乗以上であることが確定しているので、kが2の倍数であれば、pの2の指数が3以上となり8の倍数となってしまいます。
一方、kが2の倍数でなければkは2を因数に持たず、pの2の指数は2であることが確定してしまうので、8の倍数とはなりません。
つまり、kは2の倍数ではないという事が、pが8の倍数ではないという事と同じ意味を持つことになります。
倍数-基本問題2(MC1問題)
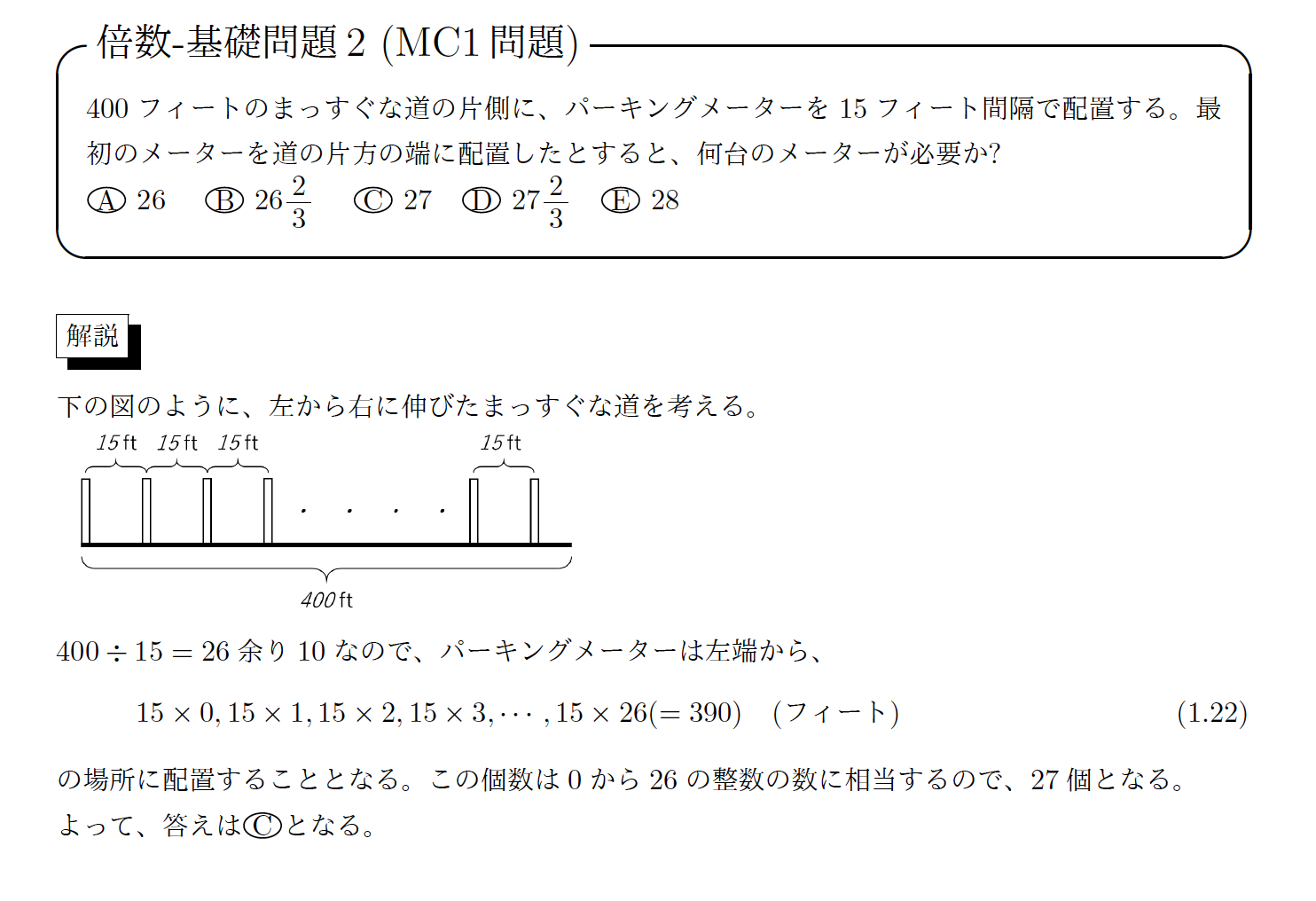
受講生の質問(1)
計算式に出てくる0.15、1.15、2.15、3…,15×26は何を示しているかが理解できません。加えて、この個数は0から26の整数の数に相当するので、27個となる。という意味合いも掴めません。
ジェイマス講師:J の回答(1)
15×0.15×1.15×2.15×3,…15×26(=390)についてですが、小数点「.」ではなく、カンマ「,」です。
パーキングメーターは左端から、0フィート、15フィート、30フィート・・・・の位置に配置されることとなります。
これを、15×0フィート、15×1フィート、15×2フィート、・・・・、15×26フィートと捉えることで、15にかけている数が0~26なので、27個あることが分かるという意味です。
[GRE数学完全攻略] 1.1.8 余り(Remainders)
p.104 基礎問題3
受講生の質問(1)
「②解説5行目の余りは14と考えるかもしれない。」までは理解できましたが、その後の下から3行目Z=20のときは余りが14、Z=10のときにxyが14になる点がなぜそうなるのかが理解できません。お手数ですが少し噛み砕いてご説明頂けますでしょうか。
ジェイマス講師:J の回答(1)
a÷bの余りを考えると余りというのはbよりの値が小さくなるということを言及しています。xy÷zにおいて、zが20である場合は、余りが14(<20)であっても問題ありませんが、zが10である場合は、余りが14(>10)というのはあり得ません。商の値を1つ増やし、余りが14-10=4となります。
p.108 応用問題4
受講生の質問(1)
3の37乗を考える場合の解説下から3行目以下、余りが0,1,2,3であるとき、10で割ると1,3,9,7になる理由、また、37÷4=9余り1なので3の37乗を10で割ったあまりは3である。という箇所がどこから数字をもってきたのかがわかりません。また、7の33乗を考える場合の下から3行の同じ箇所も理解ができません。ご説明をお願いできますでしょうか。
ジェイマス講師:J の回答(1)
(aのb乗をa^bと表すとします。)3^1, 3^2, 3^3, 3^4, ・・・・を10で割ったあまりは3, 9, 7, 1と4つの周期となるという所までは良いかと思います。
3, 9, 7, 1, 3, 9, 7, 1・・・とカウントしていき、37番目が3, 9, 7, 1のどれに該当するかというのを求めても良いのですが、
- 10で割った余りが3となるのは、1乗、5乗、9乗、・・・・と4乗置きにでてくるので、これは4で割った時余りが1の数とグルーピングできます。
- 同様に、10で割った余りが9となるのは、2乗、6乗、10乗、・・・・と4乗置きにでてくるので、これは4で割った時余りが2の数とグルーピングできます。
- 10で割った余りが7となるのは、3乗、7乗、11乗、・・・・と4乗置きにでてくるので、これは4で割った時余りが3の数とグルーピングできます。
- 10で割った余りが1となるのは、4乗、8乗、12乗、・・・・と4乗置きにでてくるので、これは4で割った時余りが0の数とグルーピングできます。
- そして、37については4で割った余が1なので、一番上のケースにグルーピングされるという意味です。
[GRE数学完全攻略] 1.1.14 倍数(Multiples)
倍数-応用問題1
受講生の質問(1)
解説のDで、「x>yなので、xがyの倍数となるケースを考える。」とあるのですが、なぜですか?
ジェイマス講師:J の回答(1)
x+yがxで割り切れるときは、x+yのx部分がxで割り切れるので、明らかにyがxで割り切れるときとなりますが、x>yなのでこのような数は存在しません。
次に、x+yがyで割り切れるときは、 x+yのy部分がyで割り切れるので、 明らかにxがyで割り切れるときとなり、x>yなのでxがyの倍数のときx+yがyで割り切れることとなります。
[GRE数学完全攻略] 1.2 分数 (Fractions)
分数-応用問題 11


受講生の質問(1)
B,Cの変形手順が分からないです。
具体的には、Bで言えば、7+5a / 8+5aの式が、1+{7+5a-(8+5a) / 8+a}へと変形です。
ジェイマス講師:J の回答(1)
分母・分子の両方にaが入っており、aを動かすと分母も分子も動いてしまうので、分子からaを消してしまおうという発想です。
Bに関しては、分母、分子共にaの係数が5であるので、分母の1倍の値を分子からくくり出せば、aが消えるます。一旦式に1を足して、分数の分子から分母の1倍を引くことでaを消去しています。
Cの式は、分子が13+2a、分母が6+aとなっております。
分子からaを消去することを考えると、分子をx(6+a)+y、つまり分母のx倍と数字yに分けることができれば、x(6+a)+yを6+aで割ると、x(6+a)/(6+a) + y/(6+a)=x+y/(6+a)と分子から、aを消去することができます。
13+2a=x(6+a)+yを考えると、aの係数が等しいので、xは明らかに2ですね。
13+2a=2(6+a)+yを考えるとy=1と計算できますよね。
よって、(13+2a) / (6+a) = (2(6+a) + 1) / (6+a) = 2 + 1/(6+a)と計算することができます。
分母と分子のaの係数の比率がxになると最初から分かっていると、テキストの書き方となります。
[GRE数学完全攻略] 1.3 指数と根(Exponents and Roots)
根-応用問題5
受講生の質問(1)
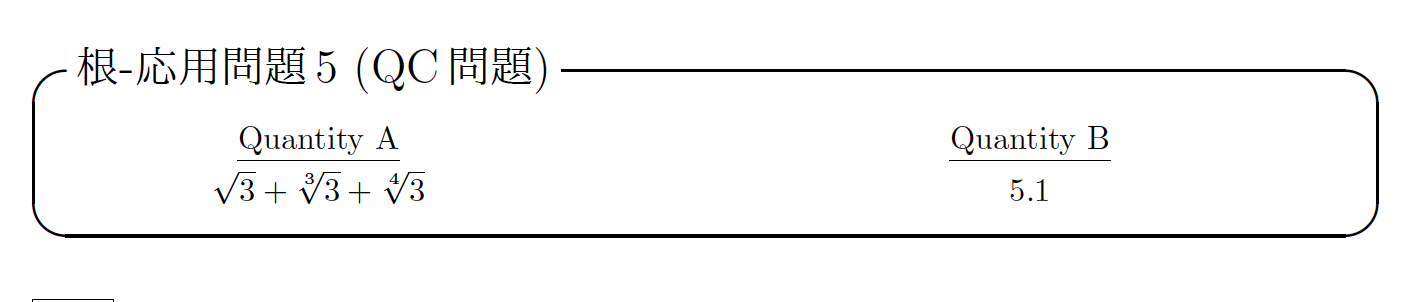
何故以下の抜粋した解説の赤枠のように、これらの根号が比較に出てくるのかがよく分かりません。
ジェイマス講師:J の回答(1)
√3 + 3√3 +4√3と5.1の比較をしております。
√3 については、1.732….と概算値を知っているので、3√3, 4√3の値の情報をどこまで得る事ができるかが勝負です。
1.6を3乗すると3を超える事から、3√3については1.6より小さいことが分かります。
4√3についても、1.5の4乗、1.6の4乗と調べる事で、小数第一位まで持った数のどのような値より小さいか分かりますが、4√3 < 3√3なので、√3 + 3√3 +4√3 < √3 + 3√3 +3√3 = √3 + 2×3√3と置き代えたもので評価してやっても、√3 + 3√3 +4√3が5.1より小さいことが偶々分かったのです。
もちろん、 4√3の値を1.5の4乗、1.6の4乗と調べ地道に評価しても構いません。
[GRE数学完全攻略] 1.6 比(Ratios)
比–応用問題8


受講生の質問(1)
セダン台数に関する式(1.162)が、xではなくyの式に変形されたコツ?見分け方?が知りたいです。
最初に30x+29y=440を見たときに、X区画のトラック台数を知りたいので、30x=440-29yと考えました。
ジェイマス講師:J の回答(1)
30x+29y=440という式から、(x, y)の組み合わせを求める方法かとおもいます。
基本的には、x, yの前の2つの係数30, 29の大きな方(この場合は係数が30であるx)を0, 1, 2, 3….と代入していく方が、440に到達するまで調べる回数が少なくなることから、29y = 440 -30xと変形し、xに値を入れていきyを求めるというのが基本です。
本問においては、29が素数であることに注目しています。
440-30xがらある整数がくくり出せるのであれば、それが29の倍数であることはまれで、それ以外の数であれば、yがくくり出した整数の倍数であると考えれば、調べる数が格段に減るよね~と考えました。
[GRE数学完全攻略] 1.7 百分率(Percent)
百分率–応用問題9


受講生の質問(1)
式(1.200)内のq(q*50/100*5/100)=1,000の展開が、q^2*50*5=1,000*100^2となる流れが分かりません。
恐らく50/100と5/100の100をそれぞれくり出した?と思いますが、その流れを教えてください。
ジェイマス講師:J の回答(1)
ここは分母を払おうという発想だけです。
左辺の、50/100の分母を払う為には左辺を100倍、5/100の分母を払う為には左辺を100倍すればよいことが分かります。
なので、右辺にも100倍×100倍を行えば、等式を保ちつつ分母を払う事ができるので、このような計算を行っただけです。
[GRE数学完全攻略] 4.1 場合の数 (Combinatorics)
応用問題3
受講生の質問(1)
下記の問題ですが、回答のケースだと何もうけとらない人は2人となっていますが、私は0こしか受け取らない人は2人以上の場合もあるかとおもったのですがその場合は考慮しなくてもいいのでしょうか?
例えば、リンゴ2個(リンゴ1個あまり)、桃2個、パイン1個を配り、3人がもらわない、といったケースは考えなくていいのでしょうか?解説では、何ももらわない人は2人だけで、リンゴ3個、桃2個、パイン1個を配りきってしまうケースのみでした)
問題文の「1個より多く受け取った人がいない」という条件の場合、「0個」と「1個もらう」という二つの選択肢を8人がそれぞれもっているように思いました。
ジェイマス講師:J の回答(1)
問題文に、3個のリンゴ、2個の桃、1個のパイナップルを配るとありますので、これらについては全て配る前提です。これらのうち、配らないフルーツがあることを許容するのであれば、その旨が問題文にある、または、配るフルーツの数にat least 3 applesなどat leastが含まれると思います。
応用問題5
受講生の質問(1)
添付の問題ですが、縛りの多い桁から数字を決めていかなければ理由を教えてもらえないでしょうか?
自分は、
1の位-5
10の位ー9
100の位ー7
とやって間違えました。


ジェイマス講師:J の回答(1)
記載していただいた解法では、10の位の9個の数のうち、10の位で「0」を使用しない場合は、100の位は7通りありますが、10の位で「0」を使用した場合は、100の位は8通り使えることになります。よって、10の位で何を使うかによって100の位で使える数の場合の数の数が異なります。
この様な場合分けを起こらないようにするために、縛りのきついものから決めていくのが良いです。
(もちろん縛りがきついものから決めていったとしても、場合分けをして考えなければならないような問題も存在します。)
解説も参考にしていただければ幸いです。
[GRE数学完全攻略] 4.2 確率(Probability)
基礎問題5 (MC問題)
受講生の質問
解説の中で「12個のボールを鉢の鉢の中で3つ順に並べて、前から順番に、ABCが掴むと考える」とありますが、そのように考える理由が掴めません。
緑色のボール4つからあくまでも3つを一度に選ぶので、4C3かと思うのですが、何故、順列で考えるのでしょうか。
ジェイマス講師:J の回答
本文を考える際に3人をAさん、Bさん、Cさんと区別して考えたのでこのようになります。
もちろん3人を区別せずに考えても問題ありません。
その際は、確率の分母分子ともに組み合わせとなります。
[GRE数学完全攻略] 5.1 集合 (Sets)
集合-基礎問題 2 (QC 問題)
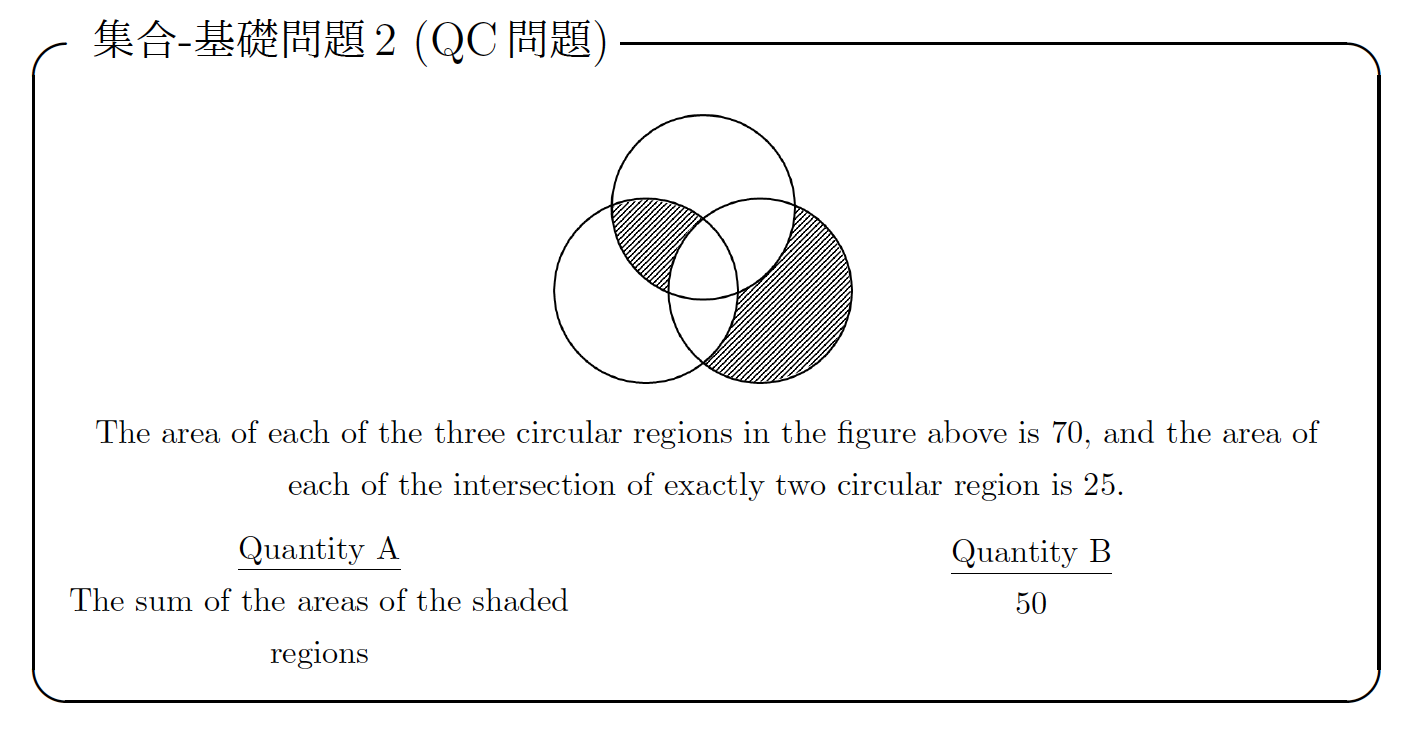
受講生の質問
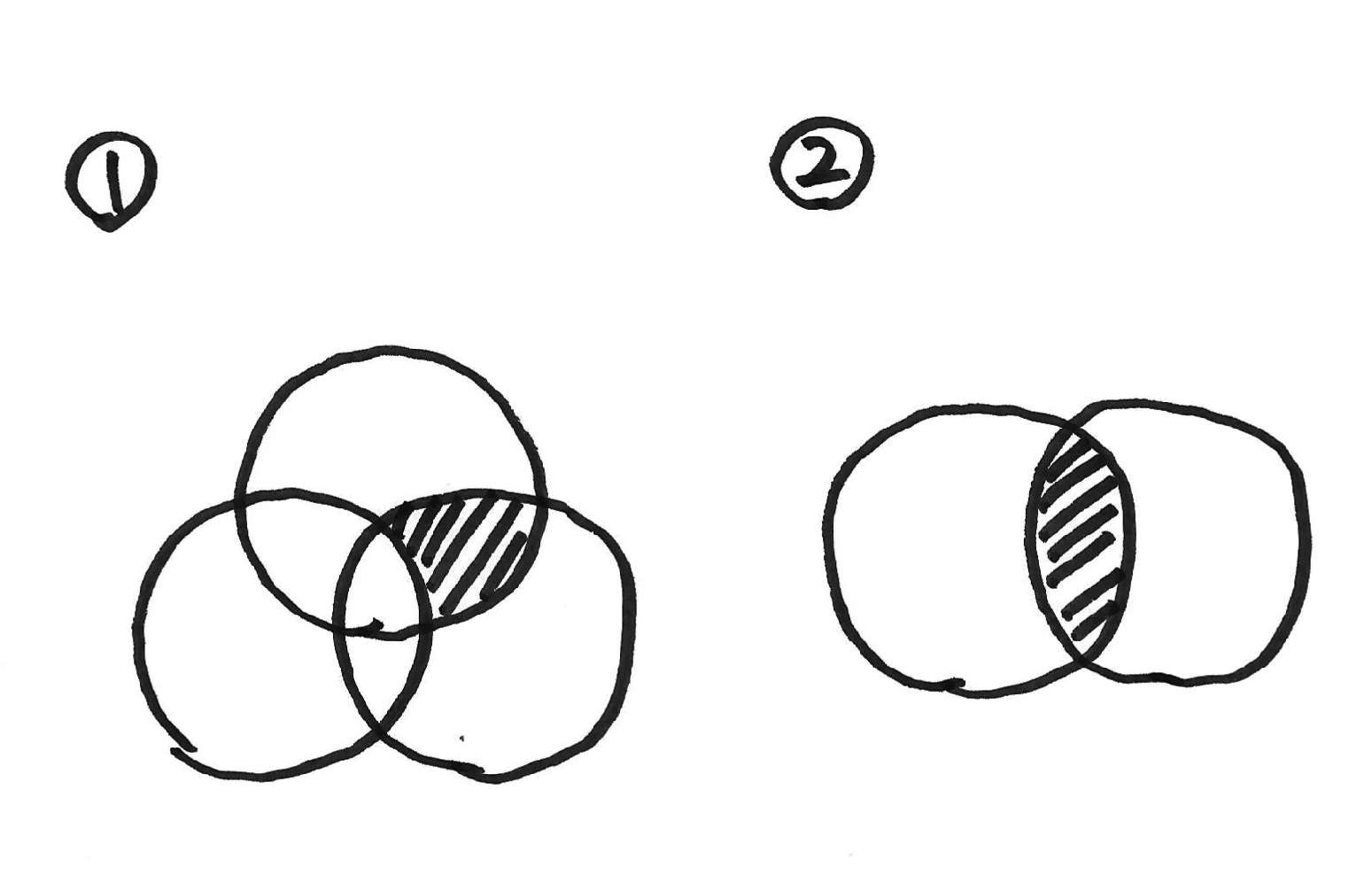
解説を読むと、問題文中の「the area of each of the intersection of exactly two circular region」(面積:25)を、下記の①と解釈していますが、英文を素直に読むと、②を指しているように考えたのですが、如何でしょうか?
また、①を指す場合と、②を指す場合で、英文がどのように異なるのか、ご教示頂けると幸いです。
ジェイマス講師:J の回答
exactlyという単語がキーワードです。
「”exactly”2つの円の領域が重なり合っている」より、2つ以上の円の領域が重なり合っていることも前提に問題文が書かれています。
とすると、①のように3つの重なり合いを想定した上で考える方が自然です。
exactlyという単語が無いとすると②という解釈ができます。






























コメントを残す