GMAT受験レポート

難易度と傾向確認のために、GMATをしたレポートになります。

受験日

• 2018年5月

本試験受験の目的

1. 1. 『GMAT数学完全攻略』対象範囲と難易度に関して、実試験との比較
   2. 『GMAT数学完全攻略』を学習してもなお、引っかかりそうな問題の調査・解説
   3. 今後の『GMAT数学完全攻略』改定案の検討

解答時間の方針

1. 1. Quantitative最初の10問は点数レンジ決定に影響するため、特に慎重に解答
   2. 問題を解く3ステップは下記に気を付けて、1問2分(実際は1分半)ペースで解く
      • 問題文の理解：特に時間をかけ読み間違いをしないように気を付ける
      • 解法の方針検討：1問あたり、5～10秒を目標（実際は2~3秒）
      • 実際に計算：計算が少し複雑になれば検算行う

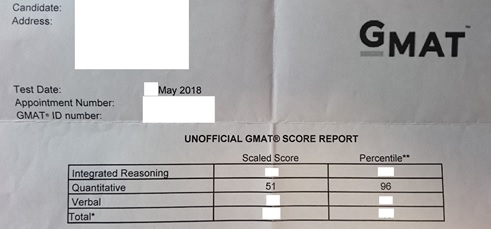
試験結果

• • Qは無事51点獲得。GMAT本試験の内容、『GMAT数学完全攻略』改定案などを考えていたため、Vは非公開。

問題概要と『GMAT数学完全攻略』の範囲比較

1. 1. 正負の問題(類題なし、基本事項のまとめあり)
   2. 不等式・因数分解（類題あり、応用問題）
   3. 指数（類題なし、指数の値が大きいので、試験では焦りから混乱する可能性あり）
   4. 鶴亀算（類題なし、連立方程式で解答可）
   5. 不等式（類題あり、応用問題）
   6. 立体（類題なし、基本事項のまとめあり）
   7. 数列（類題なし、見慣れない漸化式の解法に気付くかがポイント）
   8. 余り・指数（類題あり、応用問題）
   9. 余り（類題あり、応用問題）
   10. 割合・平均時速（類題あり、基本問題）
   11. 割合（類題あり、基本問題）
   12. 利息・複利（類題あり、基本問題）
   13. 収入・利益（類題あり、応用問題）
   14. 絶対値（類題あり、基本問題）
   15. 四角形（類題あり、基本問題）
   16. 不等式（類題なし、ひらめきが必要な超難問）
   17. 面積（類題あり、基本問題）
   18. 有理化（類題あり、基本問題）
   19. 集合(類題あり、応用問題)
   20. 座標幾何(類題あり、基本問題)
   21. 平均値(類題あり、応用問題)
   22. 百分率(類題あり、基本問題)

※その他、基礎問題レベル

試験範囲・難易度に対する考察

1. 1. 開始10問は、『GMAT数学完全攻略』の基本問題と応用問題の類題レベルが半々という印象。ステップ②に時間がけなれば10問を15分程度で解答可。
   2. 『GMAT数学完全攻略』応用問題を超える難問は1問のみ。ひらめきを必要とする問題であるため、解けなくても問題ないが、ランダムクリックしても良いかの判断ができるようになることが必要かもしれない。（開始10問が無事解答できており、かつ全体で1問のみという超難問を見極められるか）Jは、15問目頃にでたこの1問に6分程度かけてしまい、それまでのリードを全て使い切った。
   3. 『GMAT数学完全攻略』に類題がない問題は、漸化式、鶴亀算。
   4. 『GMAT数学完全攻略』の類題が9割程度。参考書の解法を確実にマスターし、解法ステップ②にかける時間をできるだけ短く、ステップ①と③にしっかり時間をかけてケアレスミスをなくせば、50点は確実。
   5. Jが回答時間に2分以上かけた問題は2問、9分程度残して終了。最初に建てた「解答時間の方針」通りに進めるには、やはり、『GMAT数学完全攻略』の解き方を覚え込み、どの類題であるかを瞬時に判別できるようになれば時間不足は防げるものと判断。（Jは英語を読む時間は決して早くはないため）

以上